ریاضی دهم انسانی فصل اول با عنوان معادله درجه دو به سه درس اصلی تقسیم بندی میشود. با توجه به توضیح مولف کتاب درسی، این کتاب از سه بخش اصلی فعالیت، کار در کلاس و تمرین تشکیل شده است؛ اما تنها چیزی که به شما میتولند کمک کند که در این درس قوی شوید و از پس آن بر آیید، بی شک حل سوال و تمرین زیاد پس از یاد گیری درسنامه است.
به طور کلی مراحل مسلط شدن به یک مبحث شامل دو مرحله اصلی اموزش و تمرین است. در ادامه به بررسی درسهای ریاضی انسانی دهم فصل اول میپردازیم.
- فصل اول ریاضی دهم انسانی
- معادله و مسائل توصیفی
- حل معادلۀ درجة ٢ و کاربردها
- روش فاکتورگیری
- روش کلی حل معادله درجه دو(روش دلتا)
- معادلههای شامل عبارتهای گویا
- گام به گام ریاضی دهم انسانی فصل اول

فصل اول ریاضی دهم انسانی
همان طور که گفته شد این درس با هدف آموزش حل، تجزیه و تحلیل معادله درجه دو تالیف شده است و تدریس را با مباحث پایه ای شروع میکند. در ادامه به سراغ بررسی تمام نکات مهم هر سه درس میرویم:
- درس اول: معادله و مسائل توصیفی
- درس دوم: حل معادلۀ درجة ٢ و کاربردها
- درس سوم: معادلههای شامل عبارتهای گویا
بیشتر بخوانید: آموزش ریاضی دهم انسانی
معادله و مسائل توصیفی
به تساوی 3𝑥 + 1 = 4 یک معادله میگوییم این تساوی به ازای 𝑥 = 1 برقرار است، هر معادلهای که دارای یک متغیر𝑥باشد را به صورت 𝑓(𝑥) = 0 مینویسیم، منظور از ریشه یک عبارت مقادیری از 𝑥 است که در معادله صدق میکند.
معادلات درجه اول
هر معادله به صورت 𝑎𝑥 + 𝑏 = 0 که در آن 𝑎, 𝑏 اعداد حقیقی و 𝑎 مخالف صفر است را معادله درجه اول مینامند.
برای درک بهتر درس، به حل چند مثال میپردازیم:
مثال1: اگر به 3 برابر عددی 7 واحد اضافه کنیم، حاصل 5 واحد کمتر از آن عدد میشود، آن عدد کدام است؟
پاسخ: اگر عدد مورد نظر را 𝑥 بگیریم، طبق مراحل زیر داریم:
3𝑥 + 7 = 𝑥 − 5
3𝑥 − 𝑥 = −7 − 5
2𝑥 = −12
𝑥 = −6
مثال 2: مجموع 4 عدد زوج متوالی برابر 76 است، کوچکترین آن ها چند است؟
پاسخ: اگر چهار عدد زوج را به صورت 2𝑥, 2𝑥 + 2, 2𝑥 + 4 ,2𝑥 + 6 در نظر بگیریم، پس داریم: 2𝑥 + (2𝑥 + 2) + (2𝑥 + 4) + (2𝑥 + 6) = 76
8𝑥 + 12 = 76
8𝑥 = 64 ⇒ 𝑥 = 8
با به دست آوردن x فقط کافی است آن را در عبارات 2𝑥, 2𝑥 + 2, 2𝑥 + 4 ,2𝑥 + 6، جایگذاری کنیم. اکنون داریم:
2𝑥 = 2 × 8 = 16
2𝑥 + 4 = (2 × 8) + 4 = 16 + 4 = 20
2𝑥 + 2 = (2 × 8) + 2 = 18
2𝑥 + 6 = (2 × 8) + 6 = 16 + 6 = 22
کوچکترین عدد از بین 4 عدد بالا 16 است.
حل معادلۀ درجة ٢ و کاربردها
این مبحث یکی از مهم ترین و اساسی ترین مباحث ریاضیات پایه است. در این درس روش هایی گفته میشود که ابزار شما برای رویارویی با انواع سوالات میباشد. کتاب ریاضی دهم فصل اول انسانی در ابتدا به تعریفی از معادله درجه دو و در ادامه به مثلث خیام و اتحاد های جدید و راه های حل و تجزیه این معادلات میپردازد.
شما میتوانید به راحتی کتاب ریاضی و آمار دهم انسانی را از اینجا دانلود کنید.
ما در این مقاله به برسی برخی از مهم ترین موارد این قسمت میپردازیم:
برای حل معادله معادالت درجه 2 به فرم ax2 = + bx + c = 0 روشهای متنوعی وجود دارد. چون بیشترین توان مجهول، در این معادله 2 است، معادلات درجه 2 نامیده میشوند.
تجزیه عبارتهای جبری
یکی از روش های حل معادله درجه دو است و در این روش معادله را به کمک فاکتورگیری یا اتحادها تجزیه می کنیم تا معادله به شکل ضرب دو یا چند عبارت در بیاید و سپس تک تک عبارتها را مساوی با صفر قرار می دهیم؛ برای استفاده از این روش باید به تجزیه عبارت جبری و اتحادها تسلط کافی داشته باشید، در سال قبل با اتحادهای مهم زیر آشنا شدید:

از اتحادهای مهم دیگر که در این فصل با آنها آشنا خواهید شد، به اتحاد مکعب دو جمله ای و حالت تفاضل آن و همچنین اتحاد چاق و لاغر میتوانیم اشاره کنیم.

روش فاکتورگیری
به طور خلاصه اگر دو یا چند جمله که بین آن ها علامت جمع یا منها وجود دارد، دارای عامل مشترکی باشند، آن عامل را می توانیم از جملات بیرون آورده و به صورت حاصل ضرب بنویسیم.
روش کلی حل معادله درجه دو (روش دلتا)
گاهی اوقات نمی توان ریشه های معادله درجه 2 را به راحتی از روش تجزیه و مربع کامل کردن بدست ورد در این شرایط سراغ روش کلی حل معادله درجه 2 (روش دلتا) میرویم که در تمامی مواقع به جواب میرسد.
برای حل معادله درجه 2 استاندارد ax2 + bx + c = 0 مراحل زیر را طی میکنیم.
1) ابتداضرایب a, b, c معادله درجه 2 را مشخص میکنیم.
2) دلتا معادله را طبق رابطه ∆= b2 − 4ac محاسبه میکنیم.
3) ریشههای معادله را از رابطه زیر بدست میآوریم.
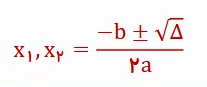
نکته :اگر ∆< 0 باشد معادله جواب ندارد، ∆= 0 باشد معادله دارای یک جواب است و اگر ∆> 0 باشد معادله دارای دو جواب است.
معادلههای شامل عبارتهای گویا
به معادلههایی که شامل عبارتهای گویا باشند معادلات گویا می گویند، برای حل معادالت گویا تمامی عبارتها را به یک طرف میبریم و سپس با مخرج مشترک گیری به یک کسرمشترک در مخرج میرسیم، سپس ریشه های صورت کسررا به دست میآوریم، از بین ریشههای صورت، آنهایی را میپذیریم که مخرج کسر را صفر نکند.
به مثال زیر دقت کنید:

اگر شما به دنبال یک منبع بی نقص برای یادگیری ریاضی دهم انسانی ریاضی فصل اول هستید، به شما خلاصه نکات ست را پیشنهاد می دهم. این خلاصه نکات به شما یک درسنامه کامل و خالص از محتوای درسی ارائه میدهد که با مثال های کافی و به جا فرایند یادگیری را آسان میکند. همچنین سه درس فصل اول، هر کدام به طور مجزا داری خلاصه نکات خود هستند تا مطالب به طور کامل و دقیق در ذهن شما جا بیوفتد.
گام به گام ریاضی دهم انسانی فصل اول
آیا واقعا گام به گام نیاز است؟ این سوالی است که باید قبل از اینکه اقدام به تهیه گام به گام ریاضی دهم انسانی فصل اول کنیم، از خودمان بپرسیم. گاهی هدفمان تنها یافتن جواب ها و تمام کردن تکالیفمان است، اما اشتباه نکنید! گام به گام ها فقط برای بررسی سوالات حل شده توسط خودمان است؛ سوالاتی که بعد از مطالعه درسنامه روی آن ها فکر کرده ایم و زمان گذاشتهایم.
نکته مهم دیگری که باید به آن توجه داشت این است که رابطهی مستقیمی بین میزان تسلط ما به دروس و تعداد سوالات حل شده ما است. هر چه در حل سوال، کمیت و مخصوصا کیفیت را بهبود ببخشیم، عمق فهم و درک ما از مبحث افزایش مییابد و شاید آن وقت گام به گام دیگر عامل چندان مهمی در رشد عملکرد تحصیلی ما به حساب نیاید.
جمعبندی
فصل اول ریاضی و آمار دهم علوم انسانی به مطالعه معادلات درجه دوم اختصاص دارد. این فصل در سه درس اصلی ارائه شده که شامل معادله و مسائل توصیفی، حل معادله درجه دوم و کاربردهای آن، و معادلات شامل عبارات گویا میباشد. تسلط بر این فصل نیازمند ترکیب یادگیری مفهومی با حل تمرینات متنوع است. به همین دلیل، روشهای مختلفی از جمله تجزیه عبارات جبری، فاکتورگیری و روش دلتا برای حل معادلات آموزش داده میشود. در نهایت، استفاده صحیح از راهنماهای حل مسئله ( گام ب گام) به عنوان ابزاری برای ارزیابی پاسخهای شخصی و تثبیت یادگیری توصیه میگردد.








2 پاسخ