ریاضی دهم تجربی فصل اول به معرفی مجموعه ها و دنباله ها که از مفاهیم پایه ای در ریاضی دهم می باشند،پرداخته است.این فصل به چهار درس تقسیم شده است و هر چهار درس به نسبت مابقی فصول و دروس ریاضی تجربی در آینده،ساده تر می باشند؛همچنین از این فصل ساده ریاضی دهم تجربی در کنکور سراسری 2 سوال طرح می شود .در این مقاله ضمن آموزش و مرور مطالب به معرفی مباحث سوال خیز ریاضی دهم تجربی فصل اول در کنکور خواهیم پرداخت.
- معرفی فصل
- عناوین درس های فصل اول ریاضی دهم تجربی
- کاربرد مجموعه ها در زندگی
- کاربرد الگو ها در زندگی
- کاربرد این فصل در کنکور
- آموزش ریاضی دهم تجربی فصل اول
- پیشنیاز ها
- درس اول ریاضی دهم:مجموعه های متناهی و نامتناهی
- مجموعه های شناخته شده
- تفاضل دو مجموعه
- بازه
- مجموعه های متناهی و نامتناهی
- درس دوم ریاضی دهم:متمم یک مجموعه
- مجموعه های مرجع و متمم مجموعه
- تعداد اعضای اجتماع دو مجموعه
- درس سوم:الگو ها و دنباله ها
- جمله عمومی
- الگوی خطی
- الگوی غیر خطی
- درس چهارم:دنباله های حسابی و هندسی
- دنباله حسابی
- حساب جمله n دنباله حسابی:
- واسطه حسابی
- دنباله هندسی
- جمله n ام هندسی
- خلاصه نکات
- کلام آخر
- سوالات متداول
معرفی فصل
عناوین درس های ریاضی دهم تجربی فصل اول
درس اول:مجموعه های متناهی و نامتناهی
درس دوم:متمم یک مجموعه
درس سوم:الگو و دنباله
درس چهارم:دنباله های حسابی و هندسی
کاربرد مجموعه ها در زندگی
مجموعه ها در ریاضی کاربردی فراتر از فصل اول ریاضی دهم تجربی و حتی دبیرستان دارند.به اذعان برخی از ریاضی دانان سرشناس:”تمامی موضوعات در جهان را می توان با دنباله ها بیان کرد” ما از مجموعه ها برای کاربردشان در منطق روزانه هم استفاده می کنیم؛برای مثال یک کلاس درس را مد نظر قرار دهید،فرض کنید که دبیر شما می خواهد بداند چه کسانی در درس زیست و چه کسانی در درس شیمی مهارت دارند. ممکن است برخی در شیمی،زیست،هر دو و هیچکدام مهارت داشته باشند.شما برای بیان حالات ممکن در این واقعیت می توانید از مجموعه ها استفاده کنید! این یکی از کاربرد های بسیار ساده مجموعه ها در زندگی می باشد.
کاربرد الگو ها در زندگی
کمی با دقت بیشتری به دنیای پیرامون خود نگاه کنید؛طرح های فرش،ظروف چیده شده و… تمام این ها مثال هایی ساده از الگو ها هستند. اما از خود می پرسید:”من چطور میتوانم در ریاضی این الگو ها را ببینم” در نگاه اول الگو ها بسیار ساده به نظر می رسند مانند:اعداد زوج-فرد-طبیعی و… اما بسیاری از الگوهای پیچیده وجود دارند که حتی در زمینه هایی مانند بورس و صنعت کاربرد دارند.همچنین الگو ها باعث افزایش دقت و تفکر ریاضی می شود که در ادامه مسیر دبیرستان و زندگی کاربرد دارند.

کاربرد فصل اول ریاضی دهم در کنکور
کنکور سراسری بودجه بندی مشخصی را هر ساله ارائه می کند و در آخرین بودجه بندی از ریاضی دهم تجربی فصل اول،2 سوال در نظر گرفته شده است که با توجه به سهولت این درس،می تواند به بالا بردن درصد ریاضی تجربی ها کمک کند.
آموزش ریاضی دهم تجربی فصل اول
در این بخش قبل از پرداختن به آموزش فصل اول ریاضی دهم،میخواهیم کمی به مرور نکات درس داده شده در پایه های گذشته بپردازیم.
پیشنیاز ها
قبل پرداختن به درس اول میخواهیم برخی از نکات را از سال پیش یا سال جاری عنوان کنیم که به شما در پیشبرد فصل کمک خواهد کرد.
نمایش اعضای مجموعه در {} اتفاق می افتد.
اعضای مجموعه با ویرگول(،) از یکدیگر جدا می شوند.
.نماد (عضویت) برای نمایش عضو بودن در یک مجموعه و نماد(عدم عضویت) برای نمایش عدم عضویت در یک مجموعه استفاده می شود.
.نماد (زیر مجموعه) برای نمایش زیر مجموعه بودن استفاده می شود
برخی از مجموعه های مشهور:
مجموعه اعداد طبیعی:N={1,2,3,4,…}
مجموعه اعداد حسابی:W={0,1,2,3,4,…}
مجموعه اعداد صحیح:Z={…,-1,0,1,…}
مجموعه اعداد گویا:Q={m/n|,n∈Z ,N≠0}
مجموعه اعداد گنگ:Q‘=R-Q
از نماد [] برای بازه های بسته و از () برای بازه های باز استفاده می شود.
اجتماع:وقتی مجموعه ها را با یکدیگر ترکیب می کنیم.
اشتراک:زمانی که فقط موارد مشترک میان مجموعه ها را میخواهیم
اجتماع را با نماد(اجتماع) و اشتراک را با نماد(اشتراک) نمایش میدهیم
مجموعه تهی:مجموعه که هیچ عضوی ندارد و زیر مجموعه تمام مجموعه ها می باشد.
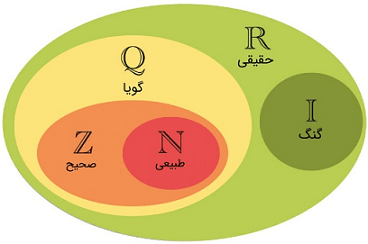
درس اول: مجموعه ها متناهی و نامتناهی
مجموعه های شناخته شده:
با توجه به موارد پیش نیاز میتوانیم نتیجه بگیریم که:مجموعه اعداد طبیعی تا حقیقی
با توجه به اینکه تاکنون تمامی اعدادی که فرا گرفتیم از زیرمجموعه های اعداد حقیقی می باشند،هر نقطه در محور اعداد یک عدد حقیقی به حساب می آید.
تفاضل دو مجموعه:
نماد – نشان دهنده تفاضل دو مجموعه می باشد. برای مثال دو مجموعه با نام های a و b را در نظر بگیرید که:
a={1,2,3,4,5}
b={2,3,4}
a-b=1,5
حالا شما بگویید (N)-(W)=؟
همانطور که می دانید اعداد حسابی شامل تمام اعداد مثبت و صفر میشود،اعداد طبیعی هم شامل تمام اعداد مثبت می باشد.پس تنها عاملی که اعداد حسابی نسبت به طبیعی بیشتر دارند عدد 0 است.
بازه یا فاصله:
ما میتوانیم بی نهایت عدد میان دو عدد مانند دو و یا سه بگوییم. پس اگر بخواهیم تمام اعداد بین دو عدد را بنویسیم و یا در حل مسئله از آن استفاده کنیم، باید تمام آن ها را در برگه خود بنویسیم؟
مسلما این کار را نمی کنید.
برای نمایش این مورد ما از بازه ها به شکل زیر استفاده می کنیم.
حال اگر بخواهیم خود عدد را هم شامل شود نقطه را توپر و اگر نخواهیم خود عدد در درون بازه باشد نقطه آن را خالی می گذاریم.
اما بیان ساده تری برای آن وجود دارد که از شکل زیر برای نمایش آن استفاده می کنیم.
به بازه هایی که خود عدد را شامل نمی شوند بازه باز و به مواردی که خود عدد را شامل می شوند بازه بسته می گویند.
البته نوع دیگری از بازه ها وجود دارند که یک سر آنها یک عدد و سر دیگر آنها محدودیتی ندارد،به زبانی دیگر بینهایت است.برای مثال زمانی که شما می گویید هر کسی که سنش از 18 سال بالاتر است،محدودیتی برای سن تعریف نکرده اید، پس یک بازه نیم باز را مطرح کرده اید.
مجموعه های متناهی و نامتناهی:
شما چند عدد می توانید بین 1و2 بگویید؟
یا چند عدد می توانید میان 1.1 و 1.2 بگویید؟
حتی نمی توانیم آنها را بشماریم!
در معنای لغوی نامتناهی یعنی انتها ندارد،یعنی قابل شمارش نیست. پس دریافتیم که مجموعه هایی که تنها اعضای آن قابل شمارش باشد متناهی است.
برای مثال مجموعه اعداد اول دو رقمی قابل شمارش است اما مجموعه اعداد اول بزرگتر از 3 خیر؟
درس دوم :مجموعه مرجع و متمم مجموعه
کلاس خود را در نظر بگیرید. اگر هر موجودیتی مانند کتاب-دانش آموز-میز و… را یک مجموعه در نظر بگیرید، یک مجموعه ای وجود دارد که تمام آن موجودیت ها در آن عضو هستند به نام:کلاس.
در ریاضیات به مجموعه هایی که مانند کلاس در مثال بالا عمل می کنند را مجموعه مرجع می نامیم و با نماد U آن را نشان می دهیم.
حال فرض کنید ما مجموعه انسان های درون کلاس را مورد بحث قرار می دهیم. در این مورد ما این مجموعه را مجموع مرجع در نظر می گیریم. فرض کنید که در کلاس ما مجموعه دانش آموزان،مجموعه معلم و مجموعه ولی را داریم.
اگر ما از مجموعه افراد درون کلاس را کم کنیم چه مواردی برای ما می ماند؟ معلم و ولی.
به معلم و ولی در مثال بالا متمم مجموعه می گوییم.
متمم مجموعه از رابطه زیر بدست میاید.
A‘=U-A
به زبان ساده متمم مجموعه یعنی: هر چیزی که در مجموعه وجود ندارد ولی در مجموعه مرجع وجود دارد.
تعداد عضو های اجتماع دو مجموعه:
مثال زیر را در نظر بگیرید:
دانش آموزان یک مدرسه در کلاس های والیبال و فوتبال ثبت نام کرده اند. ما با دانستن تعداد نفرات هر کلاس و تعداد نفرات مشترک می توانیم با قاعده ای که در زیر آمده است،مجموع نفرات حاضر در دو کلاس را بگوییم:
n(AUB)=(n(A) + n(B))-n(AuB)
درس سوم:الگو و دنباله
جمله عمومی:
عبارتی جبری که با داشتن آن میتوان بدون دانستن مقدار قبلی،مقدار جمله nرا به دست آورد. برای مثال الگوی زیر را در نظر بگیرید:
1,3,5,7
با کمی تفکر متوجه شدیم که عدد هر مرحله از جمع شماره جمله با عدد 2 به دست میاید. حالا شما بگویید جمله 20 این دنباله چه عددی دارد.
الگوی خطی:
الگو هایی که هر عدد ، به مقداری ثابت به نسبت عدد قبلی خود بزرگتر است. برای مثال مجموعه اعداد فرد را در نظر بگیرید، در این مجموعه هر عضو به نسبت عضو قبلی 2 عدد بزرگتر است.
الگو های خطی شباهت بسیاری به معادله خط دارند،به طوری که از فرمول آنها برای حساب جمله عمومی الگوی خطی استفاده می کنیم.
در نتیجه به هر الگویی که از طریق فرمول زیر عدد n به دست می آید الگوی خطی می گوییم:
Tn=an+b که در آن n شماره جمله مورد نظر و a,b اعدادی حقیقی،دلخواه و ثابت هستند.
الگوی غیر خطی:
در این الگو ها نسبت افزایش عدد به نسبت عدد قبلی ثابت نمی باشد.
دنباله:
هر تعداد عددی دلخواه که پشت سر هم قرار بگیرند.
توجه داشته باشید که هر الگویی دنباله است اما برعکس این جمله صادق نمی باشد.
درس چهارم: دنباله های حسابی و هندسی
دنباله حسابی:
به دنباله هایی گفته می شود که با افزوده شدن یک عدد ثابت به عدد قبلی خودش به دست می آید. همچنین به آن اعداد ثابت قدر نسبت نیز می گویند.
حساب جمله n دنباله حسابی:
Tn=t1+(n-1)d
در مثال بالا t1 اولین جمله و d قدر نسبت می باشد.
واسطه حسابی:
اعداد 50 و 20 را در نظر بگیرید.حال میخواهیم سه عدد را به گونه ای انتخاب کنیم که هر 5 جمله در کنار یکدیگر تشکیل یک دنباله حسابی بدهند. به آن سه عدد واسطه ، واسطه حسابی می گوییم.
دنباله هندسی:
دنباله ای است که در آن هر جمله ای به جز جمله اول از حاصل ضرب جمله قبلی در عددی ثابت و غیر صفر بدست میاید.این عدد ثابت هم قدر نسبت نام دارد. همچنین عدد اول نیز نمی تواند صفر باشد.
جمله n ام دنباله هندسی:
Tn=t1rn-1
عبارت بالا به عنوان ضابطه جمله n در دنباله هندسی می باشد که در آن t1جمله اول و r قدر نسبت می باشد.
خلاصه نکات ریاضی دهم تجربی فصل اول
در این بخش به مرور موارد مهم ریاضی دهم تجربی فصل اول خواهیم پرداخت.
.نمایش اعضای مجموعه در {} .
.اعضای یک مجموعه با ویرگول(،) از یکدیگر جدا می شوند.
.نماد (∈) و نماد(∉) برای نمایش عضویت و عدم عضویت .
.نماد (⊆) برای زیر مجموعه
برخی از مجموعه های مشهور:
مجموعه اعداد طبیعی:N={1,2,3,4,…}
مجموعه اعداد حسابی:W={0,1,2,3,4,…}
مجموعه اعداد صحیح:Z={…,-1,0,1,…}
مجموعه اعداد گویا:Q={m/n|,n∈Z ,N≠0}
مجموعه اعداد گنگ:Q‘=R-Q
مجموعه اعداد حقیقی:R=Q∪Q‘
از نماد [] برای بازه های بسته و از () برای بازه های باز استفاده می شود.
اجتماع:وقتی مجموعه ها را با یکدیگر ترکیب می کنیم.
اشتراک:زمانی که فقط موارد مشترک میان مجموعه ها را میخواهیم
اجتماع را با نماد(اجتماع) و اشتراک را با نماد(اشتراک) نمایش میدهیم
مجموعه تهی(∅):مجموعه که هیچ عضوی ندارد و زیر مجموعه تمام مجموعه ها می باشد.
تفاضل دو مجموعه:هر چیزی که در مجموعه اول وجود دارد که در مجموعه دوم وجود ندارند.
بازه ها:روش نمایشی برای فاصله میان دو یا چند عدد.
انواع بازه:باز،بسته،نیمه باز
بازه های متناهی:بازه هایی که اعضای شما قابل شمارش باشد.
بازه های نامتناهی:اعضای آن غیر قابل شمارش است.
مجموعه مرجع:مجموعه ای که تمام مجموعه های مورد بحث زیر مجموعه آن باشند.
متمم مجموعه:هر چیزی که در مجموعه نباشد و در مجموعه مرجع باشد.
تعداد اعضای اجتماع دو مجموعه:n(A∪B)=(n(A) + n(B))-n(A∩B)
جمله عمومی:عبارتی جبری که به کمک آن میتوان جمله n یک مجموعه را بدست آورد.
الگوی خطی:الگو هایی که اختلاف دو جمله متوالی در آن ثابت است.
جمله n ام دنباله خطی:Tn=an+b
الگوی غیر خطی:الگو هایی که اختلاف دو جمله متوالی در آن ثابت نیست.
دنباله حسابی:دنباله هایی که افزوده شدن عددی ثابت به عدد قبلی به دست میاید.
قدر نسبت حسابی:عددی ثابت که به جمله قبلی برای ساخت جمله جدید استفاده می شود.
واسطه حسابی: چندین عدد بین دو عدد که با یکی دیدن تمام آنها دنباله ای حسابی ساخته می شود.
دنباله هندسی:دنباله ای که هر عدد در آن از ضرب عدد قبلی در عددی غیر از صفر و ثابت به دست میاید.
جمله n ام دنباله هندسی:Tn=t1rn-1
کلام آخر:
در این مقاله سعی شد تا ضمن آموزش و مرور ریاضی دهم تجربی فصل اول شما را با برخی از کاربرد های آن آشنا سازیم.مهمترین نکته در درس ریاضی مطالعه و تمرین بسیار می باشد.
1-تفاوت فصل اول ریاضی دهم و تجربی در چیست؟
بنا به صلاح دید وزارت آموزش و پرورش این دو کتاب با یکدیگر تفاوتی ندارند.
برای مشاهده تفاوت های ریاضی رشته های انسانی و ریاضی – بر روی لینک زیر کلیک کنید
2-اهمیت این فصل در کنکور چقدر می باشد؟
این فصل به رغم سادگی درای دو سوال در کنکور سراسری می باشد.
3-چه نکاتی از این درس تست خیز هستند؟
عموما مباحث مجموعه ها و دنباله های هندسی در این چند ساله زیاد تکرار شده اند.
4-چگونه در این درs به تسلط کامل برسم؟
شما می توانید با تهیه ویدئو آموزشی زیر به تسلط بسیار خوبی در مباحث برسید.







