با یک مقاله آموزشی دیگر در خدمت شما دوستان عزیز هستیم. این بار با آموزش فصل دوم ریاضی نهم. در این پایه، فصل دوم ریاضی نهم با عنوان اعداد حقیقی، یکی دیگر از فصل های مهم این بخش است؛ چرا که درک درست از مفاهیم اعداد حقیقی پیش نیاز بسیاری از دروس ریاضیات دبیرستانی و پیش دانشگاهی است. ما سعی می کنیم ابتدا جایگاه این فصل را توضیح دهیم، سپس هر یک از مفاهیم آن را به طور جداگانه ای بررسی بررسی کنیم.
ریاضی در هر مقطعی نه فقط یک مجموعه فرمول ها و محاسبات خشک است؛ بلکه درسی است برای تفکر های منطقی و استدلال های زیبا. بسیاری از دانش آموزان فکر می کنند این درس را می توانند با حفظ کردن فرمول ها بیاموزند. اما این درس فرا تر از دروس حفظیاتی شماست. در این مقاله در کنار آموزش ریاضی نهم فصل دوم می کوشیم این دیگاه را عوض کنیم و با درکی بهتر به یادگیری این درس شیرین برویم.
آنچه در ادامه مطالعه می کنید:
- خلاصه فصل دوم ریاضی نهم
- اعداد گویا
- اعداد حقیقی و گنگ
- قدر مطلق
خلاصه فصل دوم ریاضی نهم
در این بخش می خواهیم به تدریس فصل دوم ریاضی نهم بپردازیم. برای این کار اول باید با مفاهیم کلی درس آشنا شویم. مجموعه اعداد حقیقی، شامل اعداد گویا و گنگ، گسترده ترین مجموعه عددی است که دانش آموزان در مدرسه با آن آشنا می شوند. تمام اعدادی که بتوان آن ها را روی محور عددی نشان داد، عضوی از مجموعه اعداد حقیقی هستند؛ اعم از اعداد طبیعی، اعداد کسری(گویا) و یا اعداد رادیکالی و ریشه ها(گنگ).
بیشتر بخوانید: آموزش ریاضی نهم درس اول

درس اول، فصل دوم ریاضی نهم (اعداد گویا)
هدف این درس: دانش آموزان مفهوم عدد گویا را بدانند و بتوانند آن ها را تشخیص دهند، آن ها را روی محور عددی نمایش بدهند و محاسبات مربوط به آن ها را بتوانند انجام دهند.
اعداد گویا
در پاسخ به سوال اعداد گویا چه اعدادی هستند باید گفت؛ عدد گویا، عددی است که بتوان آن را به صورت یک کسر نوشت. همانند کسر زیر:
p/q
که در آن p و q اعداد صحیح هستند و q هیچ گاه نمی تواند صفر باشد.
مثال:
5 , 6- , 3/4 , 9/5-
نکته: حتی عدد های صحیح (مثل 4 و یا 1-) هم عدد گویا محسوب می شوند چون آن ها را هم می توان به حالت یک کسر نوشت.
1/1- , 4/1
در ادامه مباحثی چون تعیین علامت اعداد گویا، مقایسه اعداد گویا، نوشتن کسر بین دو کسر، محاسبات عبارت های اعداد گویا و انواع اعداد گویا مباحث ارائه شده در درس اول است که شما می توانید با مراجعه به خلاصه نکات ریاضی فصل 2 فروشگاه ست به تمامی این آموزشات دسترسی پیدا کنید.
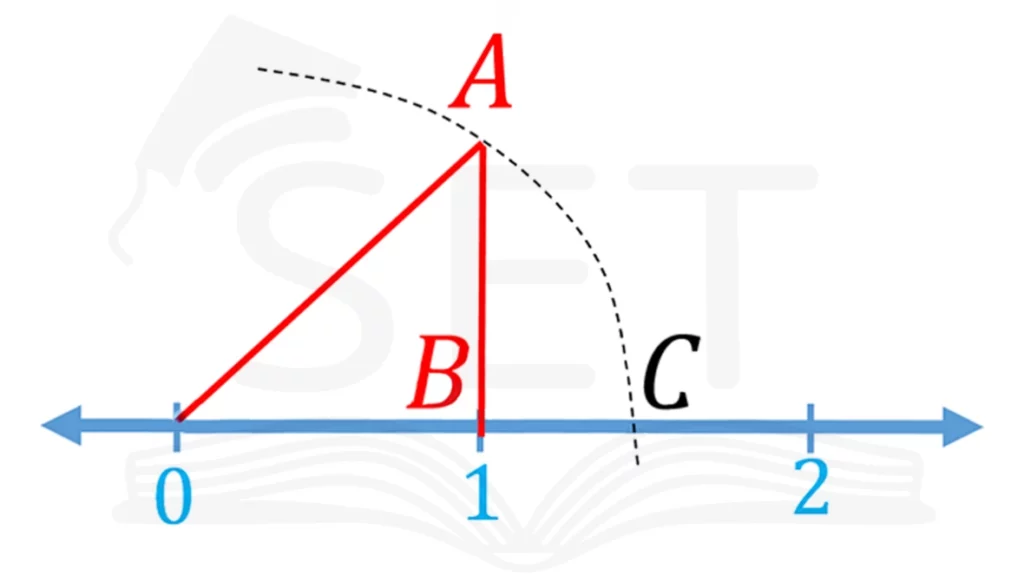
درس دوم، فصل دوم ریاضی نهم (اعداد گنگ و اعداد حقیقی)
هدف این درس: آشنایی با مجموعه اعداد حقیقی، نحوه مقایسه، نمایش و درک ارتباط با مجموعه خای دیگر. به زبان ساده یاد می گیریم عدد حقیقی یعنی چه و چطور تمام اعدادی که تا به امروز آموختیم در آن جای می گیرد.
اعداد حقیقی چه اعدادی هستند
اعداد حقیقی به هر عددی گفته می شود که بتوان آن را روی محور اعداد نشان داد. این اعداد شامل دو دسته اعداد گویا و اعداد گنگ می شوند. به عبارتی اعداد حقیقی از اجتماع مجموعه ی اعداد گنگ و گویا
Q U I = R
تفاوت اعداد گویا و گنگ
| ویژگی | عدد گویا | عدد گنگ |
|---|---|---|
| شکل نمایش | به صورت q/p | قابل نوشتن به صورت کسر نیست |
| نمایش اعشاری | مختوم و متناوب | نا مختوم و نا متناوب |
| مثال | 2/5 = 0.4 | …1.4142135 = 2√ |
| کاربرد | در محاسبات ساده | در اندازه گیری های دقیق |
نمایش اعداد حقیقی بر روی محور اعداد
در محور اعداد حقیقی، هر نقطه به یک عدد حقیقی مربوط می شود و بر عکس، هر عدد حقیقی یک نقطه روی محور دارد. عدد های مثبت بعد از صفر، اعداد منفی قبل صفر و خود صفر شامل این اعداد می شود. بین هر دو عدد حقیقی، بی نهایت عدد حقیقی دیگر وجود دارد. این به دلیل پیوستگی مجموعه اعداد حقیقی است. مثال
بین 1 و 2 عدد هایی مانند 1.3 ، 1.45 ، 2√ ، 1.86 و بی نهایت عدد ححقیقی دیگر وجود دارد.
نکته: در صورتی که نیاز به حل تمرین و نمونه سوال برای تقویت محارت های ریاضی در این بخش ها را دارید بهتر است، نمونه سوال حل شده ریاضی فصل دوم ما را تهیه کنید. این نمونه سوالات با جواب حل شده هستند و شما را در یادگیری حل سوالات این بخش یاری میکند.

درس سوم، فصل دوم ریاضی نهم (قدر مطلق و تقریب)
هدف این درس: شناخب قدر مطلق و یادگیری روش محاسبه آن، یادگیری نوشتن اعداد حقیقی به صورت تقریبی، آشنایی با مفهوم خطای تقریب
قدر مطلق
قدر مطلق هر عدد حقیقی فاصلهی آن عدد از صفر روی محور عددی است، بدون توجه به جهت (مثبت یا منفی). یعنی فقط بزرگی عدد مهم است، نه علامتش. به عبارت دیگر اگر محور عددی را رسم کنیم، قدر مطلق هر عدد برابر است با فاصلهی آن عدد تا صفر.
نماد قدر مطلق:
∣a∣
محاسبهٔ تقریبی عددهای حقیقی
در محاسبه برخی از اعداد گنگ، اعشاری بی پایان به دست می آید که عملا نوشتن آن را نا ممکن می کند. در این زمان برای نوشتن مقدار این اعداد از تقریب استفاده می کنیم تا بتوانیم در محاسبات از آن ها استفاده کنیم. تقریب روش های مختلفی دارد. از انواع آن می توان به:
گرد کردن:
در این روش عدد را تا رقم دلخواهی (مثلاً تا دهم، صدم یا هزارم) نگه میداریم و طبق قاعده آن عدد را می نویسیم. قاعده گرد کردن: اگر رقم بعدی کمتر از 5 باشد حذف می شود و اگر خود 5 یا بیشتر بود یک واحد به رقم قبلی اضافه می شود.
مثال:
2.24⇒ 2.23607 (تقریب تا صدم)
قطع کردن:
این روش مشابه روش قبلی است فقط بدون استفاده از قاعده آن. یعنی فقط اعداد را تا اعشار مد نظر نوشته.
مثال:
3.14⇒3.14159(تقریب تا صدم)
خطای تقریب
وقتی عددی را تقریب می زنیم، همیشه مقدار واقعی و مقدار تقریبی کمی فرق دارند. به این تفاوت خطای تقریب میگوییم. برای محاسبه مقدار خطای تقریب از فرمول زیر استفاده می کنیم:
خطای تقریب=∣مقدارواقعی−مقدارتقریبی∣
مثال:
1.41≈2√
…1.41142=2√
پس: خطا = ∣1.4142−1.41∣ = 0.0042
سخن پایانی
در پایان فصل دوم ریاضی نهم، درمییابیم که مفهوم «عدد» بسیار گستردهتر از آن چیزی است که در ابتدا تصور میکردیم. از اعداد طبیعی و صحیح گرفته تا گویا و گنگ، همه در مجموعهی بزرگتری به نام اعداد حقیقی گرد هم آمدهاند؛ مجموعهای که با آن میتوان هر نقطهای روی محور عددی را نشان داد. در این فصل یاد گرفتیم که چگونه با اعداد گویا و گنگ کار کنیم، آنها را روی محور نمایش دهیم، مقایسه کنیم و با مفاهیمی همچون قدر مطلق و تقریب آشنا شدیم. درک درست از این فصل، پلی است برای ورود به مباحث مهمتر ریاضی در پایههای بالاتر، مانند عبارتهای جبری، معادلات، توابع و هندسه تحلیلی.
امیدوارم این مقاله برای شما دانش آموزان عزیز مفید واقع شود.








3 پاسخ